Software Rasterization: Primitives I

So far we worked with rectangles (aka quads) which is two triangles, but world is way more than that we have lines, circles, curves, and even polygons. That's where we introduce primitives. 

Lines:

Let's start by the most simple primitives so far. Lines are tricky because if you think about we can draw a simple one pixel line. But who does that in 2025? We need to have thickness and maybe make the color with gradients. That's where the magic happens. Instead of drawing it as pixels, Let's draw lines as quads, How? if you look closely to any line you can see it's a  small  rectangle because it has no curves it's a line. 

Before we step into the algorithm we need first to know what is a normal and what's perpendicular 

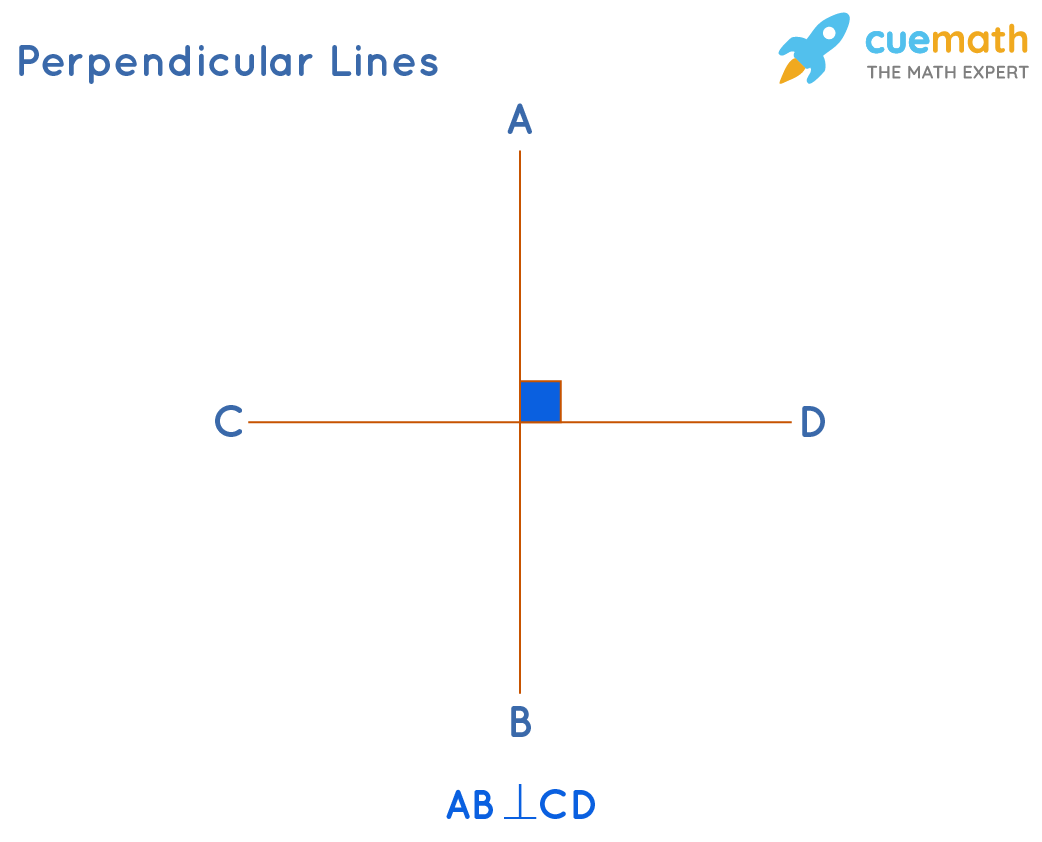
 What does perpendicular mean?

Let's say we have vectors $u$ and $v$. We can say they are perpendicular if they meet at a $90^{\circ}$ angle.

Now, What's a normal?

A normal vector is a vector that's perpendicular to another vector. It's commonly used to describe the orientation or direction  of where the vector goes

How will we use this in our line?

To draw a line, we basically need three things: the start point $a$, the end point $b$, and the thickness (width) $w$. We also know that a quad is made of four vertices and six indices that connect these vertices in order to form a rectangle. That means our goal is to figure out four points that we can use as the quad’s vertices. Let’s go through the math step by step (already explained above in the interactive guide, but here are the details specific to our line):

Step 1:

First, we need the direction of the line: $$ \overrightarrow{d} = b - a = (b_x - a_x, b_y - a_y) $$ Then we normalize $\overrightarrow{d}$, because we only care about its direction (not its length). This avoids scaling issues.

Step 2:

Next, we calculate the perpendicular vector: $$ \overrightarrow{n} = (-d_y, d_x) $$ We do this by rotating the direction vector by $90^{\circ}$ to get a perpendicular vector.

Step 3:

Our normal vector $\overrightarrow{n}$ has length 1 (since we normalized $\overrightarrow{d}$). Now we scale it by $w / 2$.

Why divide by 2? Because we’ll be offsetting in both directions. This way, the distance between the two parallel edges of the quad will equal the full width $w$.

Step 4:

Finally, we compute the four vertex positions. For each point ($a$ and $b$), we create two vertices by moving the point along $\pm \overrightarrow{n}$:

$$ \begin{align*} v_0 &= a + \overrightarrow{n} \\ v_1 &= b + \overrightarrow{n} \\ v_2 &= a - \overrightarrow{n} \\ v_3 &= b - \overrightarrow{n} \end{align*} $$

These four vertices form a quad that represents our thick line.

Implementation 

I will try to make the implementation as minimal as possible just for the showcase and as I said earlier that I will refactor my code at some point and add my local git repo to GitHub. 

Anyways, Let's start with another two pairs primitives.h and primitives.cpp

primitives.h

#pragma once
#include <vector>

#include "Vertex.h"

struct Line {
    std::vector<Vertex> vertices;
    std::vector<int> indices;
};

Line drawLine(Point p0, Point p1, int width, Color color);

Let's now start implementing our drawLine function inside primitives.cpp

#include <primitives.h>

Line drawLine(Point p0, Point p1, int width, Color color){
    Line line;
    line.vertices.resize(4);
    line.indices.resize(6);
   // Impl goes here
    return line;
}

We resize vertices by four as we only have four vertices and indices by 6 as it requires 6 vertices to draw a quad (2 triangles)

We need to implement a new function called normalize to normalize our direction vector. Let's create a new header called helpers.h

#pragma once
#include <cmath>

inline Point normalize(const Point &v) {
    float len = std::sqrt(v.x * v.x + v.y * v.y + v.z * v.z);
    if (len == 0.f) return {0.f, 0.f};
    return {v.x / len, v.y / len};
}

Now, Let's calculate the direction and the normal vectors

auto direction = normalize(p1 - p0);
auto n = Point(-direction.y, direction.x);

Now, we need to scale the normal vector with our width divided by 

n = n * (width / 2.0f);

Now, it's time to calculate our vertices and add inside our vertices vector

Point v0 = p0 + n;
Point v1 = p1 + n;
Point v2 = p0 - n;
Point v3 = p1 - n;
line.vertices[0] = {v0, color};
line.vertices[1] = {v1, color};
line.vertices[2] = {v2, color};
line.vertices[3] = {v3, color};

Last step would be add indices inside the vector

//Triangle One
line.indices[0] = 0;
line.indices[1] = 1;
line.indices[2] = 2;
//Triangle Two
line.indices[3] = 1;
line.indices[4] = 2;
line.indices[5] = 3;

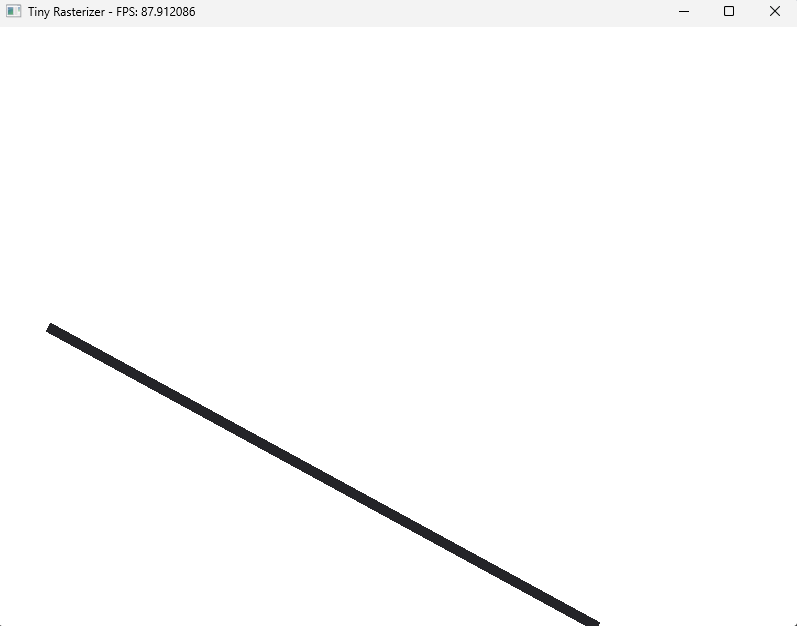
Let's now use our line and draw it inside our main.cpp

while(running){
        // Other stuff....
        auto line = drawLine({50, 300}, {600, 600}, 10, {128, 128, 128, 255});
        draw_indexed(pixels, width, height, line.vertices, line.indices, image);
        // Other stuff....
}

If everything works as expected you should see this